Funciones lineales (rectas)

Función a partir de dos puntos

Si tenemos dos puntos de la recta, podemos calcular la expresión algebraica de la función. Sólo tenemos que sustituir las coordenadas de los puntos en la forma general de la función

y resolver el sistema de ecuaciones.

Ejemplo

Vamos a calcular la función lineal que pasa por los puntos $(1,2)$ y $(2,7)$.

Tenemos que hallar la pendiente, $m$, y la ordenada, $n$.

Primer punto

Como $x=1$ e $y=2$, sustituyendo,

Segundo punto

Como $x=2$ e $y=7$, sustituyendo,

Tenemos el sistema

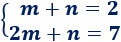
Resolviendo el sistema, por ejemplo, por reducción, tenemos que $m=5$ (con lo que $n=-3$). Por tanto, se trata de la función

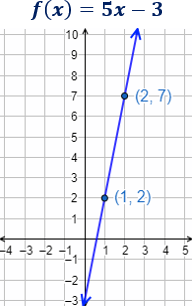
Intersección de dos funciones

Si tenemos dos funciones lineales, podemos preguntarnos si las rectas que representan se cortan y en qué punto lo hacen.

Para responder esta pregunta, sólo tenemos que igualar las dos expresiones algebraicas y resolver la ecuación.

Ejemplo

Vamos a calcular el punto de corte de las dos siguientes rectas:

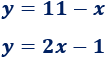
Como $y=y$, igualando,

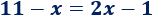
Resolvemos la ecuación:

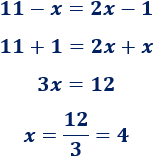
La primera coordenada del punto de corte es $x=4$. La segunda coordenada la obtenemos calculando su imagen en alguna de las dos rectas:

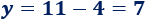
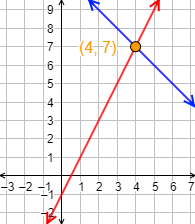
Por tanto, el punto de corte es $(4,7)$.

Gráfica:

Paralelas y perpendiculares

Dos rectas son paralelas si no se cortan en ningún punto (o si son iguales). Esto ocurre cuando tienen la misma pendiente, $m$.

Dos rectas son perpendiculares si se cortan formando un ángulo recto (ángulo de 45°). Las rectas perpendiculares a la recta con pendiente $m$ son las que tienen pendiente $-1/m$.

Ejemplo

Las siguientes rectas son paralelas porque tienen la misma pendiente ($m=2$):

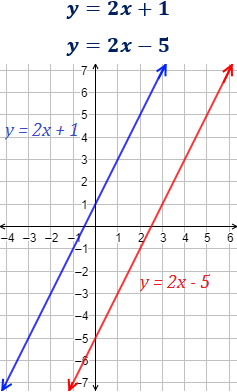
Las siguientes rectas son perpendiculares porque la pendiente de la una es el opuesto del inverso de la pendiente de la otra:

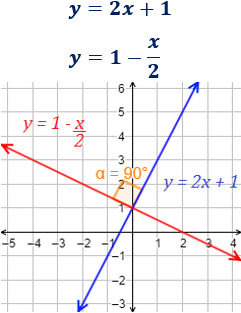
EJEMPLO:

Problema 1

Las pendientes de tres rectas son $m_1=1$, $m_2=-2$ y $m_3=3$.

¿Cuál de ellas crece más rápidamente? ¿Cuál de ellas es una recta decreciente?

SOLUCIÓN

R//La recta decreciente es la que tiene la pendiente negativa, $m_2$.

Las otras dos rectas son crecientes y crece más rápido la que tiene pendiente $m_3$.

Problema 2

Hallar, si existe, el punto de corte de las siguientes rectas:

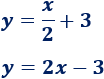
¿Son rectas paralelas o perpendiculares?

SOLUCIÓN: 

Igualamos las funciones para calcular el punto de corte:

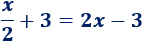
Resolvemos la ecuación:

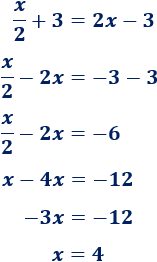
Calculamos $y$ a partir de $x$:

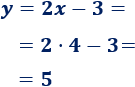
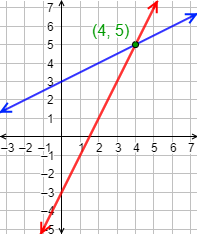
Las rectas se cortan en el punto $(4,5)$.

Como se cortan, no pueden ser paralelas.

Tampoco son perpendiculares porque las pendientes son positivas (es indispensable tener pendientes de signo contrario para ser perpendiculares).

Gráfica:

ACTIVIDAD: Resolver los siguientes ejercicios en su cuaderno.

1) Hallar, si existe, el punto de corte de las siguientes rectas:

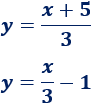
¿Son rectas paralelas o perpendiculares?

2) Calcular y representar la función cuya gráfica es una recta que pasa por los puntos (1,2)(1,2) y (−3,4)(−3,4). ¿Cuál es su pendiente?