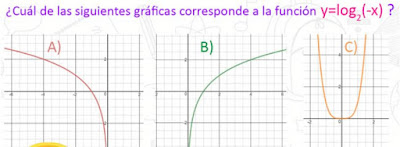
FUNCIÓN LOGARÍTMICA

Una función logarítmica está formada por un logaritmo de base a, y es de la forma:

siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.

Cuando 0 < a < 1, entonces la función logarítmica es una función decreciente y cuando a > 1, entonces es una función creciente.

La función logarítmica es la inversa de la función exponencial.

Y, cuando 0 < a < 1:

Características

• Dominio: 
  El dominio son todos los números reales positivos.
• Recorrido: 
  El recorrido son todos los números reales.
• Derivada de la función logarítmica: 
• Las funciones logarítmicas son continuas.
• Si a es mayor que 1 (a > 1), la función es estrictamente creciente. En cambio, si a es menor que 1 (a < 1), la función es estrictamente decreciente.
  
• La imagen de 1 siempre es 0 y la imagen de a es 1.
  
  Así pues, las funciones logarítmicas siempre pasan por los puntos (1 , 0) y (a , 1).
  
• La función logarítmica es inyectiva.

Propiedades

Todas las funciones logarítmicas cumplen las siguientes propiedades:

1. Función logarítmica del producto:
   
2. Función logarítmica de la división:
   
3. Función logarítmica del inverso multiplicativo:
   
4. Función logarítmica de la potencia:
   

Logaritmos

Sean dos números reales a y b, siendo a ≠ 1. El logaritmo en base a de b es el elemento al que hay que elevar el número a para dé como resultado el número b.

Por ejemplo, el logaritmo en base 3 de 9 es 2, ya que siendo a = 3 y b = 9, el número al que hay que elevar 3 para que dé 9 es 2, 3² = 9.

Cuando el logaritmo es en base 10 (a = 10), se llama logaritmo decimal y no se suele escribir la base: f(x) = log x. También se llaman algoritmos comunes.

Normalmente, cuando no se especifica la base, se entiende como función logarítmica la que tiene de base el número e (a = e = 2,7182818…). En este caso se llama logaritmo neperiano (o logaritmo natural) y suele escribirse: f(x) = ln x.

Ejemplo 1

Supongamos que tenemos la función logarítmica con a = 2, definida por la función:

La función es continua en todos los números reales positivos.

Como a = 2 > 1, la función es creciente.

Como podemos ver en su gráfica, la función pasa por los puntos (1 , 0) y (2 , 1).

Ejemplo 2

Grafique la función y = log 10 ( x – 1) + 2.

Comience con la gráfica logarítmica básica y = log b x . Luego cambie la gráfica 1 unidad a la derecha y 2 unidades hacia arriba.

ACTIVIDAD: realiazar un resumen en su cuaderno del tema, responder la siguiente incognita.

Función cuadrática

Una función cuadrática (o parabólica) es una función polinómica de segundo grado. Es decir, tiene la forma

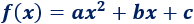
siendo $a\ne 0$.

Esta forma de escribir la función se denomina forma general.

La gráfica de una función cuadrática siempre es una parábola.

Ejemplo

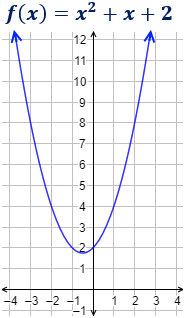
Las parábolas tienen forma de $\cup$ (si $a>0$) o de $\cap$ (si $a<0$).

Además de la orientación, el coeficiente $a$ es la causa de la amplitud de la función: cuanto mayor es $|a|$, más rápido crece (o decrece) la parábola, por lo que es más cerrada.

Vértice

Las funciones cuadráticas tienen un máximo (si $a<0$) o un mínimo (si $a>0$). Este punto es el vértice de la parábola.

La primera coordenada del vértice es

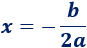
Y la segunda coordenada es su imagen:

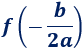
Ejemplo

Calculamos el vértice de la función

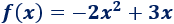
Identificamos los coeficientes:

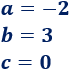
Como $a$ es negativo, la parábola tiene forma de $\cap$. El vértice es un máximo.

La primera coordenada del vértice es

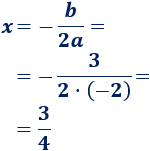
Calculamos la segunda coordenada:

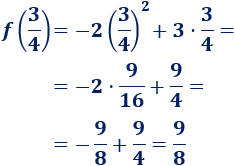
Por tanto, el vértice es el punto

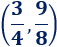
Gráfica:

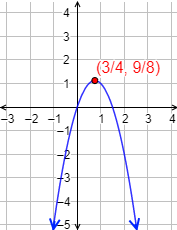
 Puntos de corte con los ejes

Una parábola siempre corta el eje de ordenadas (eje Y) en un punto. Como esto ocurre cuando $x=0$, se trata del punto $(0,c)$ puesto que $f\left(0\right)=c$.

Una función corta al eje de abscisas cuando $y=0$. Por tanto, para hallar estos puntos de corte, tenemos que resolver una ecuación cuadrática:

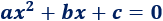
Como una ecuación cuadrática puede tener una, dos o ninguna solución, puede haber uno, dos o ningún punto de corte con el eje X.

Recordamos la fórmula que necesitamos:

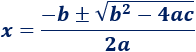
Ejemplo

Calculamos los puntos de corte de la función

Los coeficientes de la ecuación son $a=1$, $b=0$ y $c=-1$.

Eje Y:

El punto de corte con el eje Y es $(0,-1)$.

Eje X:

Resolvemos la ecuación de segundo grado:

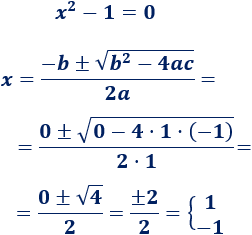
Hay dos soluciones: $x=1$ y $x=-1$.

La segunda coordenada es $0$.

Por tanto, tenemos los puntos de corte

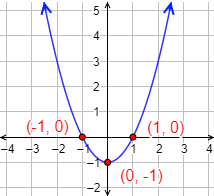
Gráfica:

Formas factorizada y canónica

La forma factorizada de una función cuadrática es

donde $a$ es el coeficiente principal (visto anteriormente); $x_1$ y $x_2$ son las soluciones de la ecuación $a{x}^2+bx+c=0$.

• Si la ecuación $a{x}^2+bx+c=0$ no tiene soluciones, no podemos factorizar la función.
• Si la ecuación sólo tiene una solución, $x_1$, la forma factorizada es $f\left(x\right)=a(x-x_1{)}^2$.

Ejemplo

En el ejemplo anterior vimos que los puntos de corte con el eje X de la función $f\left(x\right)=x^2-1$ son $(1,0)$ y $(-1,0)$. Por tanto, la forma factorizada de esta función es

La forma canónica de una función cuadrática es

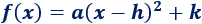
donde $a$ es el coeficiente principal visto ya; $h$ es la primera coordenada del vértice y $k$ es la segunda.

Ejemplo

Vimos en un ejemplo que el vértice de la función $f\left(x\right)=-2x^2+3$ es $(3/4,9/8)$. Por tanto, su forma canónica es

Intersección de dos parábolas

Podemos preguntarnos si las gráficas de dos funciones se cortan entre sí. Para resolver esta pregunta, tenemos que igualar las funciones y resolver la ecuación resultante.

Ejemplo

Calculamos la intersección de las siguientes parábolas:

Igualamos ambas funciones y resolvemos la ecuación:

Las soluciones de la ecuación son $x=1$ y $x=-1$.

La segunda coordenada se obtiene calculando la imagen:

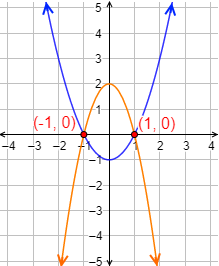
Por tanto, los puntos de corte son $(1,0)$ y $(-1,0)$.

Gráfica:

EJEMPLOS;

Problema 1

Calcular el vértice de la siguiente función parabólica:

SOLUCIÓN

Los coeficientes son $a=-3$, $b=6$ y $c=5$.

La primera coordenada del vértice es

Calculamos la segunda coordenada:

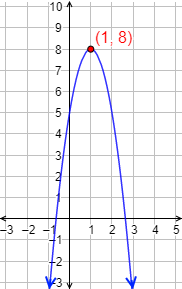
Por tanto, el vértice es el punto $(1,8)$.

Gráfica:

Problema 2

Determinar los puntos de corte de la parábola

Y el vértice de la parábola

SOLUCIÓN 

La forma factorizada nos facilita calcular los puntos de corte con el eje X:

Punto de corte con el eje Y (sustituimos $x=0$):

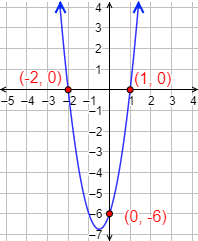
Por tanto, es el punto $(0,-6)$.

Gráfica de $f$:

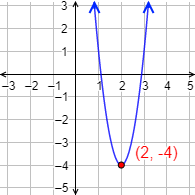
La forma canónica de la función $g$ nos proporciona las coordenadas de su vértice: $(2,-4)$.

Gráfica de $g$:

ACTIVIDAD: Realizar los siguientes ejercicios en su cuaderno tomar foto y enviarla. 

1) Calcular los puntos de intersección de las siguientes funciones:

2) Determinar los puntos de corte y el vértice de la siguiente función:

3) Determinar los puntos de corte y el vértice de la siguiente función: